|
1. ARIMA
Autoregressive Integrated Moving Average
(ARIMA)
atau biasa disebut dengan metode Box-Jenkins. ARIMA sangat baik ketepatannya
untuk peramalan jangka pendek, yang tidak membentuk suatu model struktural baik
itu persamaan tunggal atau simultan yang bebasis kepada teori ekonomi atau logika,
namun dengan menganalisis probabilistik atau stokastik dari data deret waktu (time
series) dengan menggunakan nilai masa lalu dan sekarang dari variabel
dependen untuk menghasilkan peramalan jangka pendek yang akurat dengan
mengabaikan variabel independennya. Hal ini terjelaskan dengan prinsip dari
metode ini yaitu “let the data speak for themselves”.
read more
read more
Metode peramalan dengan menggunakan ARIMA dapat kita
jumpai dalam peramalan ekonomi, analisis anggaran, kontrol terhadap proses dan kualitas,
analisis sensus, perubahan struktur harga industri, inflasi, indeks harga saham,
perkembangan nilai tukar terhadap mata uang asing dsb.
Beberapa
keuntungan yang dapat diperoleh dengan menggunakan ARIMA:
1)
Merupakan model tanpa teori karena variabel yang digunakan adalah nilai-nilai lampau
dan kesalahan yang mengikutinya.
2)
Memiliki tingkat akurasi peramalan yang cukup tinggi karena setelah mengalami
pengukuran kesalahan peramalan mean absolute error, nilainya mendekati
nol.
3)
Cocok digunakan untuk meramal sejumlah variabel dengan cepat, sederhana, akurat
dan murah karena hanya membutuhkan data variabel yang akan diramal.
Model ARIMA menggunakan pendekatan iteratif dalam
indentifikasi terhadap suatu model yang ada. Model yang dipilih diuji lagi
dengan data masa lampau untuk melihat apakah model tersebut menggambarkan
keadaan data secara akurat atau tidak. Suatu model dikatakan sesuai (tepat)
jika residual antara model dengan titik-titik data historis bernilai kecil,
terdistribusi secara acak dan bebas satu sama lainnya.
Pemilihan model terbaik dapat dilakukan dengan
membandingkan distribusi koefisien-koefisien autocorrelation (otokorelasi)
dari data time series tersebut dengan distribusi teoritis dari berbagai
macam model.
2. KLASIFIKASI
MODEL ARIMA
Metode ARIMA dibagi kedalam tiga kelompok model time
series linier, yaitu autoregressive
model (AR), moving average model (MA) dan model campuran yang
memiliki karakteristik kedua model di atas yaitu autoregressive integrated
moving average (ARIMA).
1)
Autoregressive Model (AR)
Suatu
persamaan linier dikatakan sebagai autoregressive model jika model tersebut
menunjukkan 𝑍𝑡
sebagai fungsi linier dari sejumlah 𝑍𝑡
actual kurun waktu sebelumnya bersama dengan kesalahan sekarang. Bentuk model
ini dengan ordo p atau AR (p) atau model ARIMA (p,d,0) secara
umum adalah:
2) Moving
Average Model (MA)
Berbeda dengan moving
average model yang menunjukkan 𝑍𝑡 sebagai
fungsi linier
dari sejumlah 𝑍𝑡 aktual kurun waktu
sebelumnya, moving average
model menunjukkan
nilai 𝑍𝑡 berdasarkan kombinasi kesalahan
linier masa lalu
(lag). Bentuk
model ini dengan ordo q atau MA (q) atau
model ARIMA (0,d,q)
secara umum
adalah:
Terlihat dari model bahwa 𝑍𝑡 merupakan rata-rata tertimbang
kesalahan sebanyak q periode lalu yang digunakan untuk moving average
model. Jika pada suatu model digunakan dua kesalahan masa lalu maka
dinamakan moving average model tingkat 2 atau MA (2).
3)
Autoregressive Integrated Moving Average (ARIMA)
Sebuah model time series digunakan berdasarkan
asumsi bahwa data time series yang digunakan harus stasioner yang artinya
rata-rata variasi dari data yang dimaksud konstan. Tapi hal ini tidak banyak
ditemui dalam banyak data time series yang ada, mayoritas merupakan data yang
tidak stasioner melainkan integrated. Data yang integrated ini harus
mengalami proses random stasioner yang seringkali tak dapat dijelaskan dengan
baik oleh autoregressive model saja atau moving average model saja
dikarenakan proses tersebut mengandung keduanya. Oleh karena itu campuran kedua
model yang disebut autoregressive integrated moving average (ARIMA)
menjadi lebih efektif menjelaskan proses itu. Pada model campuran ini series
stasioner merupakan fungsi linier dari nilai lampau beserta nilai sekarang dan
kesalahan lampaunya. Bentuk umum model ini adalah:
Proses
autoregressive integrated moving average secara umum dilambangkan dengan
ARIMA
(p,d,q), dimana:
Ø p
menunjukkan ordo/derajat autoregressive (AR)
Ø d adalah
tingkat proses differencing
Ø q menunjukkan
ordo/derajat moving average (MA).
3. TAHAPAN ARIMA
(Box-Jenkins)
Langkah-langkah
penerapan metode ARIMA secara berturut-turut adalah identifikasi model,
pendugaan parameter model, pemeriksaan diagnosa dan penerapan model untuk
peramalan. Secara lengkap dapat dilihat pada bagan di bawah ini:
1) Model umum
dan uji stasioneritas
Stasioneritas berarti tidak terdapat pertumbuhan
atau penurunan pada data. Data secara kasarnya harus horizontal sepanjang sumbu
waktu. Dengan kata lain, fluktuasi data berada di sekitar suatu nilai rata-rata
yang konstan, tidak tergantung pada waktu dan varians dari fluktuasi tersebut
atau tetap konstan setiap waktu. Untuk mengetahui stasioner tidaknya data dapat
diamati dari time. Penggunaan model untuk peramalan. Pemeriksaan (uji)
diagnosa estimasi parameter model indentifikasi model tentatif (sementara) dengan
memilih (p,d,q). Rumuskan model umum dan uji stasioneritas data ya atau tidak. Series plot
data tersebut, autocorrelation function data atau model trend linier data
terhadap waktu.
Suatu data time series yang tidak stasioner
harus diubah menjadi data stasioner, karena aspek-aspek AR dan MA dari model
ARIMA hanya berkenaan dengan data time series yang stasioner. Salah satu
cara yang paling sering dipakai adalah metode pembedaan (differencing)
yaitu menghitung perubahan atau selisih nilai observasi. Nilai selisih yang
diperoleh dicek lagi apakah stasioner atau tidak. Jika belum stasioner maka
dilakukan differencing lagi.
2) Identifikasi
model
Setelah data time series yang akan diolah langkah
berikutnya adalah penetapan model ARIMA (p,d,q) yang sekiranya cocok. Jika data
tidak mengalami differencing, maka d bernilai 0, jika data menjadi
stasioner setelah differencing ke- 1 maka d bernilai 1 dan seterusnya.
Dalam memilih dan menetapkan p dan qdapat dibantu dengan mengamati pola Autocorrelation
Function (ACF) dan Partial Autocorrelation Function (PACF) dengan
acuan sebagai berikut:
Kesalahan yang sering terjadi dalam
penentuan p dan q bukan merupakan masalah besar pada tahap ini, karena hal ini
akan diketahui pada tahap pemeriksaan diagnosa selanjutnya.
3) Pendugaan
parameter model
Ada
dua cara yang mendasar untuk mendapatkan parameter-parameter
tersebut:
Ø Dengan
cara mencoba-coba (trial and error), menguji beberapa nilai yang berbeda
dan memilih satu nilai tersebut (atau sekumpulan nilai, apabila terdapat lebih
dari satu parameter yang akan ditaksir) yang meminimumkan jumlah kuadrat nilai
sisa (sum of squared residual).
Ø Perbaikan
secara iteratif, memilih taksiran awal dan kemudian penghitungan dilakukan Box-Jenkins
Computer Program untuk memperhalus penaksiran tersebut secara iteratif.
4) Pemeriksaan
diagnosa
Dalam pemeriksaan
terhadap model ada beberapa metode yang bisa
dilakukan,
antara lain adalah:
a.
Pengujian model secara keseluruhan (Overall F test) dan pengujian masing
masing parameter model secara parsial (t-test), untuk menguji apakah
koefisien model signifikan secara statistik atau tidak baik secara keseluruhan
maupun parsial
b.Model
dikatakan baik jika nilai error bersifat random, artinya sudah tidak mempunyai
pola tertentu lagi. Dengan kata lain model yang diperoleh dapat menangkap
dengan baik pola data yang ada. Untuk melihat kerandoman nilai error dilakukan
pengujian terhadap nilai koefisien autokorelasi dari error, dengan menggunakan
salah satu dari dua statistik berikut:
dengan:
n’
= n-(d+SD)
d
= ordo pembedaan bukan faktor musiman
D
= ordo pembedaan faktor musiman
S
= jumlah periode per musim
m
= lag waktu maksimum
5) Pemilihan model terbaik
Untuk menentukan model
yang terbaik dapat digunakan standard error estimate berikut:
dengan:
Zt =
nilai sebenarnya pada waktu ke-t
𝑍
𝑡 =
nilai dugaan pada waktu ke-t
Model
terbaik adalah model yang memiliki nilai standard error estimate (S)
yang paling kecil. Selain nilai standard error estimate, nilai rata-rata
persentase kesalahan peramalan (MAPE) dapat juga digunakan sebagai bahan pertimbangan
dalam menentukan model yang terbaik yaitu:
dengan:
T
=
banyaknya periode peramalan/dugaan
6)
Penggunaan model untuk peramalan
Jika model terbaik telah ditetapkan, maka model siap
digunakan untuk peramalan. Untuk data yang mengalami differencing,
bentuk selisih harus dikembalikan pada bentuk awal dengan melakukan proses
integral karena yang diperlukan adalah ramalan time series asli. Notasi
yang digunakan dalam ARIMA adalah notasi yang mudah dan umum.
Misalkan model ARIMA (0,1,1)(0,1,1)9 dijabarkan menjadi sebuah persamaan
regresi yang lebih umum:
Nilai et+1 tidak akan diketahui, karena nilai
yang diharapkan untuk kesalahan random pada masa yang akan datang harus
ditetapkan sama dengan nol. Akan tetapi dari model yang disesuaikan (fitted
model) kita boleh mengganti nilai et
et-8 dan et-9 dengan nilai
nilai mereka yang ditetapkan secara empiris (seperti yang diperoleh setelah
iterasi terakhir algoritma Marquardt). Tentu saja bila kita meramalkan jauh ke
depan, tidak akan kita peroleh nilai empiris untuk “e” sesudah beberapa waktu,
dan oleh sebab itu nilai harapan mereka akan seluruhnya nol. Untuk nilai Z pada
awal proses peramalan, kita akan mengetahui nilai Zt, Zt-8, Zt-9. Akan tetapi sesudah
beberapa saat, nilai Z akan berupa nilai ramalan (forecasted value),
bukan nilai-nilai masa lalu yang telah diketahui. Teknik peramalan dengan
menggunakan ARIMA juga memberikan confidence interval. Jika peramalan
dilakukan jauh ke depan, maka confidence interval umumnya juga
akan makin melebar. Namun tidak demikian untuk confidence interval moving
average model murni. Peramalan merupakan never ending
process yang berarti jika data terbaru muncul, model perlu
diduga dan diperiksa kembali.







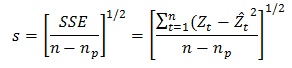



















Bagus nih, Makasih ya
Makasih artikelnya bagus, tapi bisa kasih contoh real implementasinya ga? supaya bisa lebih faham manfaat ARIMA ini. makasih
minta referensi nya dong... :)
kak kalau ARIMA (1,1,1) itu gimana rumusnya?
Bisa batu ngga ARIMA (1,1,2)(1,1,1)12